In electronics, it's essential to analyze even the simplest circuits. For basic circuits, we typically use principles like Kirchhoff's Voltage Law (KVL) and Kirchhoff's Current Law (KCL). However, when dealing with more complex circuits that have multiple controlled voltage and current sources, additional tools are required alongside KVL and KCL. Relying solely on KVL and KCL can lead to inaccurate and unreliable results. To accurately analyze such circuits and determine the various variables, methods like mesh and nodal analysis are necessary. These techniques help easily calculate unknowns such as current and voltage. In this article, we’ll take a closer look at Mesh Analysis and Super Mesh Analysis.

What is Mesh Analysis?

A mesh is essentially a loop in a circuit that doesn't contain any other loops inside it. In mesh analysis, mesh currents are used as variables instead of the actual currents, helping to simplify the overall circuit analysis. This technique requires a minimal number of equations to solve, making it more efficient. Mesh analysis relies on Kirchhoff's Voltage Law (KVL) to determine the unknown current values in the circuit.

Mesh Analysis

This method is also known as the mesh current loop technique. Once the mesh currents are found, voltage values can be calculated using Ohm’s Law. A branch is the path that connects two nodes and includes a circuit element. If a mesh has only one branch, the current through that branch is considered the mesh current. If a mesh consists of two branches, the mesh current is the sum or difference of the currents in the two loops, depending on whether they flow in the same or opposite directions.

Steps for Mesh Analysis

To determine the variables in a circuit, follow these steps when performing mesh analysis:

1. Identify the Meshes: Start by identifying the meshes in the circuit. Then, assign mesh currents, either in a clockwise or counterclockwise direction, to each mesh.
2. Determine Current Flow: For each element in the circuit, determine the current flowing through it, based on the mesh currents you've assigned.
3. Write the Mesh Equations: Write the mesh equations for each mesh by applying Kirchhoff’s Voltage Law (KVL) first, and then use Ohm's Law to relate the voltages and currents.
4. Solve the Equations: Solve the mesh equations from step 3 to find the values of the mesh currents.
5. Calculate Currents and Voltages: Once the mesh currents are known, you can calculate the current and voltage values across each element in the circuit.

General Form for Setting Up Equations in Mesh Analysis

Once the meshes in a circuit are identified, each mesh will have its own equation. These equations represent the total voltage drop across the entire loop of the mesh current. In circuits with multiple voltage and current sources, the voltage drop is calculated by multiplying the impedance of each element by the specific mesh current in the loop.

When a voltage source is inside the loop, the voltage at the source is either added or subtracted, depending on whether the voltage increases or decreases in that mesh. If a current source is present between the meshes, the mesh current will be assigned a positive or negative value based on the direction of the mesh current relative to the current source.

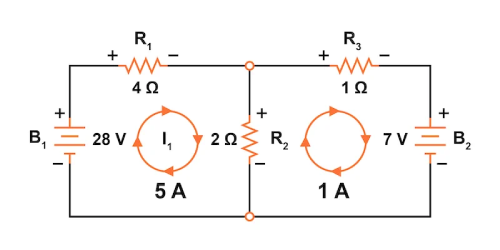
Mesh Current Method

In the circuit below, the mesh current method can be easily applied. Loop currents I1I_1I1​ and I2I_2I2​ are applied in the clockwise direction.

The polarities of the voltage drops across the resistors R1R_1R1​, R2R_2R2​, and R3R_3R3​ depend on the direction of the loop currents. In this case, I1I_1I1​ and I2I_2I2​ have opposite current flows because resistor R2R_2R2​ is shared between both loops.

With this, the polarities of the voltage drops can be determined. In practical scenarios, resistor R2R_2R2​ could be divided into two phases, but the loop currents are still used for analysis purposes. The polarities of the voltage sources remain unaffected because they are constant.

By applying Kirchhoff’s Voltage Law (KVL), the following two equations can be written:

R2(I1 – I2) + R1I1 = V1 – Derived from loop 1

R2(I2 – I1) + R1I2 = -V2 – Derived from loop 2

Once the similar terms in the above equations are combined and rearranged, the same terms appear in corresponding positions in each equation. Once the loop currents are determined, the branch currents can be calculated. The rearranged equations are:

For Loop 1:
I1(R1+R2)−I2R2=V1I_1(R_1 + R_2) - I_2R_2 = V_1I1​(R1​+R2​)−I2​R2​=V1​

For Loop 2:
−I1R2+(R2−R3)I3=−V2-I_1R_2 + (R_2 - R_3)I_3 = -V_2−I1​R2​+(R2​−R3​)I3​=−V2​

Mesh Analysis: Solved Problems

This section presents solved examples for determining the current in a circuit using the mesh current method.

In the circuit below, determine the voltage across the 15 Amp current source using mesh analysis. It is given that all elements in the circuit are current sources.

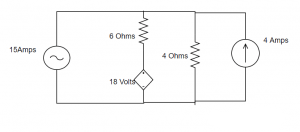
Mesh Analysis To Find Voltage

In the circuit, it's possible to convert the voltage source into a current source using a parallel resistor. To achieve this, a resistor is placed in series with the voltage source, and the resistor should have the same value as the voltage source. For example, if the voltage source is VsV_sVs​ and the resistor RsR_sRs​ has the same value, then:Vs=Is⋅Rs=4 A×4 Ω=16 VV_s = I_s \cdot R_s = 4 \, \text{A} \times 4 \, \Omega = 16 \, \text{V}Vs​=Is​⋅Rs​=4A×4Ω=16V

Now, to find the branch currents I1I_1I1​ and I2I_2I2​ for the loops, apply mesh analysis and determine the current flow directions in both loops.

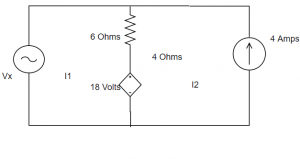
Assigning Branch Currents

Applying KVL to Each Mesh (Loop)

Mesh 1:Vx−(I1−I2)⋅18=0V_x - (I_1 - I_2) \cdot 18 = 0Vx​−(I1​−I2​)⋅18=0

Given I1=15 AI_1 = 15 \, \text{A}I1​=15A, the equation becomes:Vx+(6⋅I2)=90V_x + (6 \cdot I_2) = 90Vx​+(6⋅I2​)=90

Mesh 2:18−6⋅(I2−I1)−4⋅I2−16=018 - 6 \cdot (I_2 - I_1) - 4 \cdot I_2 - 16 = 018−6⋅(I2​−I1​)−4⋅I2​−16=0

Solving for I2I_2I2​:I2=7810=7.8 AI_2 = \frac{78}{10} = 7.8 \, \text{A}I2​=1078​=7.8A

Now, using the Mesh-1 equation to find VxV_xVx​:Vx=90−44.4=45.6 VV_x = 90 - 44.4 = 45.6 \, \text{V}Vx​=90−44.4=45.6V

This is a solved example of solving two meshes using mesh current analysis. Now, let's find the voltage and branch currents in the circuit shown below.

Mesh Current Method Across Three Meshes

Application of KVL to Each Mesh:

First Mesh:

By applying Kirchhoff's Voltage Law (KVL) to the first loop, we get:V1−R2⋅(I1−I3)−R4⋅(I1−I2)=0V_1 - R_2 \cdot (I_1 - I_3) - R_4 \cdot (I_1 - I_2) = 0V1​−R2​⋅(I1​−I3​)−R4​⋅(I1​−I2​)=0

Substituting the given values:4−2⋅I1−2⋅I3−4⋅I1−4⋅I2=04 - 2 \cdot I_1 - 2 \cdot I_3 - 4 \cdot I_1 - 4 \cdot I_2 = 04−2⋅I1​−2⋅I3​−4⋅I1​−4⋅I2​=0

Simplifying:−2⋅I3−6⋅I1=4(Equation 1)-2 \cdot I_3 - 6 \cdot I_1 = 4 \quad \text{(Equation 1)}−2⋅I3​−6⋅I1​=4(Equation 1)

Second Mesh:

Applying KVL to the second mesh:−VC−R4⋅(I2−I1)−R3⋅(I2−I3)=0-V_C - R_4 \cdot (I_2 - I_1) - R_3 \cdot (I_2 - I_3) = 0−VC​−R4​⋅(I2​−I1​)−R3​⋅(I2​−I3​)=0

Substitute for I2=−2 AI_2 = -2 \, \text{A}I2​=−2A:−VC=−4⋅I1+6⋅I2−2⋅I3=0-V_C = -4 \cdot I_1 + 6 \cdot I_2 - 2 \cdot I_3 = 0−VC​=−4⋅I1​+6⋅I2​−2⋅I3​=0

Substitute I2=−2 AI_2 = -2 \, \text{A}I2​=−2A:−VC=−4⋅I1−12−2⋅I3=0(Equation 2)-V_C = -4 \cdot I_1 - 12 - 2 \cdot I_3 = 0 \quad \text{(Equation 2)}−VC​=−4⋅I1​−12−2⋅I3​=0(Equation 2)

Third Mesh:

Applying KVL to the third mesh:−R1⋅I3−R3⋅(I3−I2)−R2⋅(I3−I1)=0-R_1 \cdot I_3 - R_3 \cdot (I_3 - I_2) - R_2 \cdot (I_3 - I_1) = 0−R1​⋅I3​−R3​⋅(I3​−I2​)−R2​⋅(I3​−I1​)=0

Substituting I2=−2 AI_2 = -2 \, \text{A}I2​=−2A:2⋅I1−8⋅I3=0(Equation 3)2 \cdot I_1 - 8 \cdot I_3 = 0 \quad \text{(Equation 3)}2⋅I1​−8⋅I3​=0(Equation 3)

Solving the Mesh Equations:

By solving the first and third mesh equations:I1=4.46 A,I3=−0.615 AI_1 = 4.46 \, \text{A}, \quad I_3 = -0.615 \, \text{A}I1​=4.46A,I3​=−0.615A

Now, substitute I1I_1I1​ and I3I_3I3​ into Equation 2 to find VCV_CVC​:VC=28.61 VV_C = 28.61 \, \text{V}VC​=28.61V

Branch Current:

The branch current IacI_{ac}Iac​ is the difference between I1I_1I1​ and I3I_3I3​:Iac=I1−I3=5.075 AI_{ac} = I_1 - I_3 = 5.075 \, \text{A}Iac​=I1​−I3​=5.075A

This is a solved example of solving three meshes using mesh current analysis. A thorough understanding of this method allows us to solve more complex circuits as well.

Super Mesh Analysis

Super mesh analysis is a more efficient approach than regular mesh analysis when dealing with large and complex circuits. In super mesh analysis, two meshes share a common component, typically a current source.

This method is similar to supernode analysis in nodal circuit analysis. It simplifies complex circuits by effectively closing voltage sources and reducing the number of reference nodes required for each voltage source. In super mesh analysis, the current source lies within the super mesh, allowing you to reduce the number of meshes by one for each current source present.

When a current source is located on the perimeter of the circuit, it might not correspond to a single mesh. In such cases, Kirchhoff's Voltage Law (KVL) is applied only to the modified meshes after simplifying the circuit.

Let’s go through an example of super mesh analysis for better understanding.

Example: Super Mesh Analysis

For the circuit below, find the values of V3V_3V3​, i1i_1i1​, i2i_2i2​, and i3i_3i3​.

1. 10i1+80(i1−i2)+30(i1−i3)=8010i_1 + 80(i_1 - i_2) + 30(i_1 - i_3) = 8010i1​+80(i1​−i2​)+30(i1​−i3​)=8060i1−20i2−30i3=8060i_1 - 20i_2 - 30i_3 = 8060i1​−20i2​−30i3​=80
2. 30=40i3+30(i3−i1)+20(i2−i1)30 = 40i_3 + 30(i_3 - i_1) + 20(i_2 - i_1)30=40i3​+30(i3​−i1​)+20(i2​−i1​)70i3−50i1+20i2=3070i_3 - 50i_1 + 20i_2 = 3070i3​−50i1​+20i2​=30
3. 15ix=i3−i215i_x = i_3 - i_215ix​=i3​−i2​i3=15ix+i2i_3 = 15i_x + i_2i3​=15ix​+i2​
4. i1=0.58 A,i2=−6.16 A,i3=2.6 Ai_1 = 0.58 \, \text{A}, \quad i_2 = -6.16 \, \text{A}, \quad i_3 = 2.6 \, \text{A}i1​=0.58A,i2​=−6.16A,i3​=2.6A
5. V3=i3⋅R3=2.6⋅40=104 VV_3 = i_3 \cdot R_3 = 2.6 \cdot 40 = 104 \, \text{V}V3​=i3​⋅R3​=2.6⋅40=104V

In this example, using super mesh analysis, we determined the values of the mesh currents i1i_1i1​, i2i_2i2​, and i3i_3i3​, as well as the voltage V3V_3V3​ in the circuit. This method is very effective in simplifying complex circuits involving current sources.

Uses of Mesh Analysis

The primary use of mesh analysis is to solve planar circuits and determine the current values at any point, whether in simple or complex electrical circuits.

Another advantage is that traditional methods for solving circuit equations can be quite challenging and often require more complex mathematical formulas. In contrast, mesh analysis simplifies the process, requiring fewer computations.

Mesh current analysis is also particularly useful in solving unbalanced Wheatstone bridges. For example:

In cases where the resistor ratios R1/R4R_1 / R_4R1​/R4​ and R2/R5R_2 / R_5R2​/R5​ are not equal, there will be some voltage and current flow through R3R_3R3​. Solving these circuits using the typical series-parallel method can be quite complicated.

To handle this, we could apply the branch current method, but this would require solving for six currents, IaI_aIa​ to IfI_fIf​, resulting in a large number of equations. This complexity can be significantly reduced with mesh current analysis, which only requires a few variables to solve.

Related Articles

Guide to Hybrid Potentiometer

Diode Dynamics: Real-World Behavior in Fast Power and RF Circuits

How Can You Fix an Oil Pressure Sensor?

Guide to Corner Reflector

Guide to 1N5408 Power Diode

What is a CMOS Sensor?

Guide to Ryzen AI Max+ 395